How To Train Your Mancala Bot
I spent the past week goofing around with genetic algorithms to develop a heuristic for evaluating a mancala board for more successful move selection. Here’s a writeup of general techniques and results.
Background
This project was for Northwestern’s EECS 348. My goal was to build a mancala bot that could beat both me and other mancala bots. The bot uses a minimax tree to select the next move, meaning it chooses the move that will produce the best outcome assuming the opponent will do the same. It recurses n levels then returns the move which will eventually produce the most desirable board state.
How the bot thinks
AB pruning is a method of ignoring board states which will never occur (if the opponent also behaves like the bot).
AB pruning assumes the following: if I’m playing a game of tic tac toe and there’s a move I can make that will make it possible for me to win, I will ignore all other moves so the bot making a decision can, too.
Here’s that example more visually (I’m X, the bot is O).
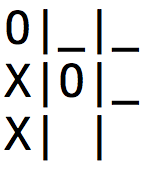
Assuming it’s my turn, the best I can do here is tie. There’s clearly a move that the bot can make next turn (bottom right) that would win the game for it—but why would I leave that space open?
The bot assumes I’m never going to choose a move that produces a desirable outcome for it, so when it’s considering previous game states it ignores any configuration where I let this happen:
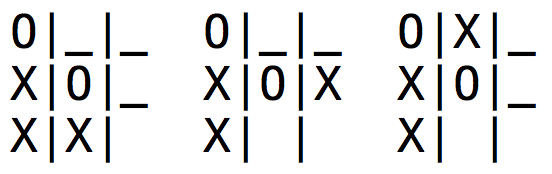
and only considers board states that follow from me making the best possible move for me.
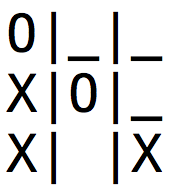
Minimax trees and AB pruning consider how good the board is for each player during their turn.
In tic-tac-toe, there are at most 9 possible moves to be made at any given time, so it’s not unreasonable to examine all possible states of the game board.
In mancala, though, there are 6 moves at any time and each move affects the remaining states of the game. That means that it’s incredibly expensive to try to look ahead to the end of the game and figure out how to get there. Instead, there needs to be a way to evaluate how good the board is at any time and just try to get to a good place. That’s where the heuristic function comes in.
A Mancala Heuristic
The function for evaluating the board state at any given time is called the heuristic function. It takes in the board state and spits out a number that expresses how good or bad the board is. A board where the bot has won should have the highest possible value, a board where it has lost should have the lowest possible value.
The problem was that I don’t know much about mancala and how to evaluate the board to determine if it’s good or not. Sure, having more pebbles in your mancala is better, but there are subtle things at play leading up to that outcome that I wasn’t sure of. I decided to let the bots learn for themselves what’s a good function or not, which is where the genetic algorithm comes in.
Genetic Algorithms
Genetic algorithms work off of principles of biology—reproduction, survival of the fittest, and genetic mutations.
The first step of this is to encode the information you need in a “chromosome”—usually a binary string or, in my case, a string of constants.
[9.2895948465511253, -5.5518479301435502, 3.7198795657176493, -4.994530957107699, 2.9397499989367311, 0.067329476348763961, -5.7550748932949647, 3.0386549697777028, 4.4171703527080091]
Next, you create a random population of chromosomes and evaluate the “fitness” of all of them. For me, I let them all play mancala against eachother and the ones who one most were most fit.
def fitness(self, p1_chromo, population):
# initialize a player with my custom chromosome
player1 = CustomPlay(1, Player.ABPRUNE, 2)
player1.score = player1.custom_score(p1_chromo)
player2 = CustomPlayer(2, Player.ABPRUNE, 2)
board = MancalaBoard()
wins = 0.0
# have p1_chromo compete against all other chromosomes
for p2_chromo in population:
player2.score = player2.custom_score(p2_chromo)
# play some games!
board.hostGame(player1, player2)
if board.hasWon(1):
wins += 1.0
board.reset()
# fitness is the proportions of wins
return wins/len(population)
Then, the most fit chromosomes are allowed to reproduce with one another, and reproduction is imitated. The chromosomes are combined and crossed over, then an element of random mutation is introduced to keep things from settling into ruts. The steps of fitness testing and reproduction are repeated until some stopping condition.
In my case, my chromosomes encoded weights for each of several attributes relevant to a game of mancala. The number of stones I had added to my mancala for a given move, the number my opponent had added, the number of stones I and my opponent had each added to our six cups and the captures that were possible, either for me or for my opponent. The board was evaluated by multiplying each of these attributes by a learned weight then adding them all up.
The genetic algorithm was able to determine which factors were most important, which were good, and which were bad. It likes adding stones to its own mancala the most and dislikes leaving captures open.
6.45 * Number of stones gained in my mancala +
-8.1 * Number of stones gained in opponent's mancala +
5.69 * Number of stones gained in my cups +
-8.9 * Number of stones gained in opponent's cups +
0.74 * Number of stones in my cup at that game state +
-7.8 * Number of stones in opponent's cups at that game state +
-5.7 * Number of captures opponent can make +
4.21 * Number of captures I can make = overall board value.
Conclusions
The actual performance of the bot is going to be decided in a tournament against other bots, but it seems that it tends to leave captures open a lot which is the primary way I beat it.
Overfitting seemed to be a big problem—after about 20 population iterations the chromosomes made bots able to beat eachother all the time or not at all which is not useful for this application. The chromosome I ultimately ended with was the result of around 6 population iterations and had a good win record with a formidable win record across the entire population at that iteration.